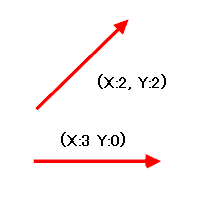
ベクトル(Vector)
ベクトルとは向きと大きさ(スカラー)を持つものを指します。
2DベクトルならX, Y。
3DベクトルならX, Y, Z。
これらの向きと大きさを持っています。
ベクトルの大きさ(スカラー)の算出
ベクトルの持っている大きさ(スカラー)とはベクトルの長さの事です。
長さを求めるには三角関数の記事で書いている2点間の距離を計算する方法を使えば算出できます。
ベクトル長さ = √ ( X² + Y² )
単位ベクトル
単位ベクトルとは大きさが1のベクトルを指します。
このベクトルは純粋に向きだけを示すベクトルになります。
正規化(Normalize)
大きさをもったベクトルを1の長さのベクトルにするのは簡単です。
ベクトルの長さでベクトルの各要素を割るだけで算出することができます。
つまり下記のような計算になります。
単位ベクトルのX = X / ベクトル長さ
単位ベクトルのY = Y / ベクトル長さ
これだけです。
難しい計算も無いので凄く簡単ですよね。
この単位ベクトルに変換する計算を正規化と呼びます。
正規化はあらゆる計算で必要になってくるので必ず覚えておきましょう!
ベクトルの数学上の表記
当たり判定等を調べていると外積と内積の計算がよく出てきます。
そういう時にベクトルは下記のように表されることが多いです。
ベクトル
ベクトルは特に特殊な書き方はされません。
ベクトル A と B があればそのまま A や B で表記されます。
※それぞれも文字の上に→が付くこともあります。
点Aと点Bをつなぐベクトルの場合は下記のような書き方をされます。
ベクトルの長さ
ベクトルの長さを示す時は|で挟んで絶対値として表記されます。
ベクトルAの長さは下記のように書きます。
|A|
これさえ覚えれば数学の式も簡単にプログラムに落とし込むことができます。
今後、色々なプログラムで必要になってくるので、思い出せないときはもう一度記事を読み直してみてください。