点と球の当たり判定
点と球の当たり判定を取るには方法について説明します。
先ず、点と球の当たり判定を取るには点と球の中心の距離を知る必要があります。
2点間の距離は三角関数を使うことで簡単に求めることができます。
距離の計算
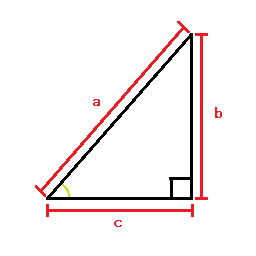
各辺の長さの2乗の合計が距離の2乗と等しくなります。
b² + c² = a²
これで長さの2乗が出ます。
後は √ a² をすれば長さが分かります。
点と円の当たり判定
先ずは2次元上で点と円の当たり判定を行います。
点(P1)が円(P2)の半径(R)に入っているかで衝突しているかが分かります。
今回の場合は下記の計算式になります。
P1(X) – P2(X) でX軸の長さP'(X)を求める
P1(Y) – P2(Y) でY軸の長さP'(Y)を求める
√(P'(X)² + P'(Y)²) = 2点間の距離
2点間の距離が半径(R)より近ければ衝突しているので
√(P'(X)² + P'(Y)²) < R
この式が成り立った場合に衝突しているという事になります。
3次元上での距離の計算
点と円で2次元上での当たり判定の取り方を記述しましたが3次元上でも基本は同じです。
XYZのそれぞれの軸に対して2乗した値の合計が距離の2乗になります。
X² + Y² + Z² = |XYZ|²
XYZ軸それぞれで2点間の距離の差を図って2乗したものを足せば距離の2乗が出ます。
これが球の半径より小さければ衝突していると判定することができます。
当たり判定の最適化
円と球の当たり判定は2点間の距離が半径より小さいかどうかで判定できました。
ただプログラム上で √ の計算をするには少しコストが掛かります。
数個の当たり判定を取る程度なら問題ありませんが、
数千数万といった当たり判定を取る必要が出てきた場合は問題になってくることがあります。
では √ をどうやって最適化すればいいでしょうか?
実は今回の場合は √ を使わないで当たり判定を取ることができます。
点と円の当たり判定
この計算式で当たり判定を取ることが出来ました。
√(P'(X)² + P'(Y)²) < R
√ を使わないという事は左側の式はこうなります。
P'(X)² + P'(Y)²
√ をしなければ単純に2乗の値になります。
こういう時は右側の値も2乗してやれば条件が同じになります。
P'(X)² + P'(Y)² < R²
こちらであればRを2乗してやるだけで比較ができます。
こうやってできる限り負荷の小さな処理にしていくことで快適で処理落ちの少ないゲームを作っていくことがプログラマーには求められています。