線分と線分の当たり判定
今回は2次元上での線分と線分の当たり判定について解説していきます。
この記事は『マルペケつくろーどっとコム』さんを参考にさせていただきました。
計算式や結果は下記の記事と同じです。
今回、こちらでは図形から外積と三角関数を使って説明していこうかと思います。
当たり判定の概要
線分同士の当たり判定はそれぞれの線分から直角三角形を作り出して導くことが出来ます。
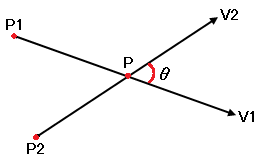
まず基本はこの図形のようになります。
P1を始点としたV1のベクトルとP2を始点としたV2のベクトルが当たっているか?
そして当たっている場合は交点Pを導きだします。
先ず、V1とV2の外積を取ることでベクトル間の角度(sinθ)を出します。
① V1 x V2 = sinθ |V1||V2|
ここでV1とV2の長さで外積の結果を割るとsinθ以外の|V1||V2|の部分を消せます。
※sinθの結果が0の場合は平行な線分同士なので当たりません。
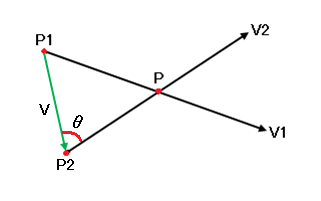
次にP1からP2へのベクトル(V)とV2の外積からの角度を求めます。
② V x V2 = sinθ |V||V2|
この外積の結果から|V2|の長さを割るとsinθ|V|となります。
この時のsinθ|V|を三角関数に当てはめると
sinθ = a / b
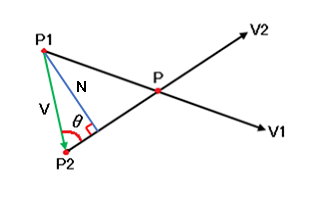
これを下記の図に当てはめるとこのようになります。
sinθ = N / |V|
つまりNについて説く式にすると
③ N = sinθ |V|
となるのでP1からV2に対して垂直な線の長さが出せます。
これが出ると更に下記の図が作れるので t1 を求める式が考えられます。
この図の内容を三角関数で式にすると下記が出ます。
sinθ = N / t1
t1について説く式に置き変えると
④ t1 = N / sinθ
これで t1 の長さが出ます。
この時の長さが 0以上でかつ、V1の長さより短ければ線分の中に納まっていることになります。
後はV2に対しても同じことをすれば両方の線分に対して当たっているかが分かります。
線分と線分の当たり判定の基本はこれで求めることが出来ます。