球と球の当たり判定

点と球の当たり判定を取るには方法については前回の記事で紹介しました。

点と球の当たり判定が取れていれば球と球も簡単に判定することができます。

b² + c² = a²

前回の2点間の距離の計算をした後に比較する対象の値が変わるだけです。

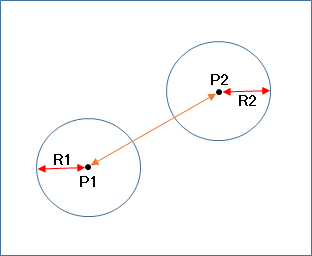
前回と同じく2次元上で円と円の当たり判定を行います。

今回は円同士なのでR1とR2の合計の長さより近いかで当たっているかが分かります。
凄く単純で分かりやすいですね。

P1(X) – P2(X) でX軸の長さP'(X)を求める
P1(Y) – P2(Y) でY軸の長さP'(Y)を求める

√(P'(X)² + P'(Y)²) = 2点間の距離

2点間の距離が半径(R1)と半径(R2)の合計より近ければ衝突しているので

√(P'(X)² + P'(Y)²) < R1 + R2

この式が成り立った場合に衝突しているという事になります。

上記の円と円の判定にZ軸を追加して計算すれば球と球の当たり判定が出来てしまします。
凄く簡単ですね！

前回はR側を2乗することで √ を無くして最適化しました。
では今回も同じように最適化してみましょう。

P'(X)² + P'(Y)² < (R1 + R2)²

今回はR1とR2の合計を2乗しています。
やっていることは同じなので難しい処理は全く必要ありません！

拡張していく時も常に最適な処理を考えて実装をしていきましょう！